先导概念
隐空间 Latent Space
一句话概括:
隐空间是压缩数据的一个表示。隐空间的作用是为了找到模式而学习数据特征并且简化数据表示。以编码器-解码器网络为例,首先使用全卷积神经网络 (FCN) 学习图片特征,我们将特征提取中对数据的降维看作一种有损压缩。但是由于解码器需要重建数据,所以模型必须学习如何储存所有相关信息并且忽略噪音。所以压缩(降维)的好处在于可以去掉多余的信息从而关注于最关键的特征。
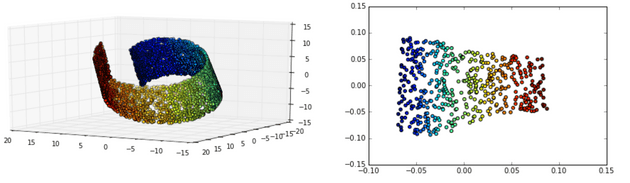
因为在隐空间中,相似样本之间特征差别作为多余信息被移除了,只有其核心特征被保留。所以当将数据点映射到隐空间后,特征相似的点距离更近。
下图将三维数据映射到了二维隐空间,隐空间内相似样本更加靠近。三维以上的隐空间很难可视化。但可以通过降维至二维或者三维进行展示。
音乐隐空间
音乐序列基本上是高维的。例如,考虑所有可能的单声道钢琴旋律的空间。在任何给定的时间,88 个键中只有一个可以按下或释放,或者播放器可以休息。我们可以将其表示为 90 种类型的事件(88 次按键,1 次释放,1 次休息)。如果我们忽略节奏,将时间量化为 16 个音符,则 4/4 时间内的两个音乐度量(小节)将有 9032 个可能的序列。如果我们把它扩展到 16 条,它将是 90256 个可能的序列。因此,我们不可能一下子处理如此多的数据,这时候就需要用到数据压缩和隐空间的概念。
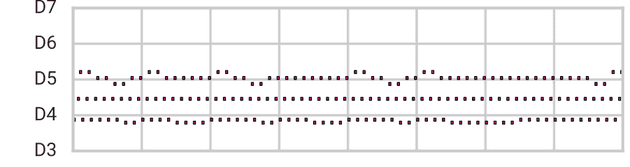
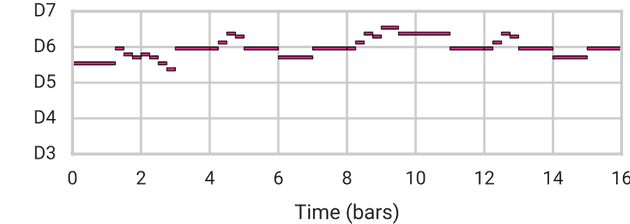
例如,这里我们展示了从 9032 个可能的 2 条序列中随机选择的钢琴 🎹 乐段。纵轴代表钢琴上的音符,横轴代表 16 个音符步数的时间。
Data Space Sample (not MusicVAE)

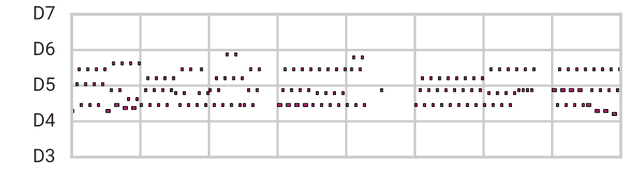
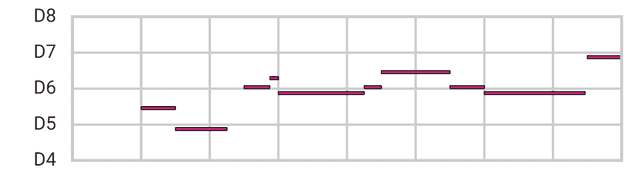
隐空间模型能够学习训练数据集的基本特征,因此可以排除这些非常规的可能性。将 2 小节旋律的隐空间中的这些点的随机样本(在本文后面描述)与之前的点进行比较:
Latent Space Sample (MusicVAE)

除了排除不现实的例子外,隐空间能够在低维空间中表示真实数据的变化。这意味着他们也可以高精度地重建真实的例子。此外,在压缩数据集的空间时,隐空间模型倾向于基于基本质量来组织数据集,将相似的示例紧密地聚集在一起,并沿着这些质量定义的向量展示变化。
隐空间的理想特性可总结如下:
表达:任何实例都可以映射到隐空间中的某个点并从中重构。
真实感:此空间中的任何点都代表一些真实示例,包括不在训练集中的示例。
平滑度:来自隐空间中附近点的示例彼此具有相似的性质。这些属性类似于艺术家的调色板,可以在调色板上探索和混合绘画的颜色选项,这些属性可以增强创造力。例如,由于表达和平滑度,类似 SketchRNN 为笔划序列学习的隐空间允许通过在隐空间中的点之间插值来重建和混合:
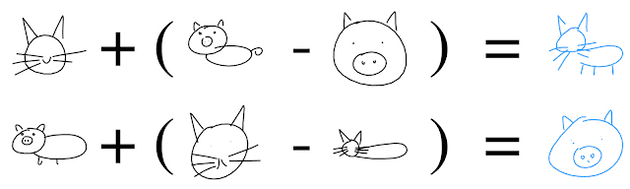
MusicVAE 要做的事就像这只 🐱 和 🐷 一样,假设它们是两个不同的乐段,我们现在需要把它们结合起来,变成一个能听的新乐段。我们还可以使用隐空间的结构来执行语义上有意义的转换,例如使用“隐约束”或“属性向量算法”。后一种技术利用了一个事实,即隐空间可以“解开”数据集中的重要品质。通过平均与共享给定质量的数据点集合(例如,猫脸草图)对应的隐向量,我们获得该属性的属性向量(“猫脸向量”)。通过从隐代码中添加和减去各种属性向量,并使用我们的模型进行解码,我们获得添加或删除相关属性的输出。我们再次用 SketchRNN 说明这一点:
学习音乐隐空间
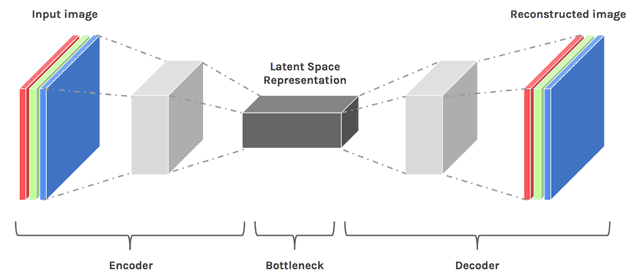
自动编码器
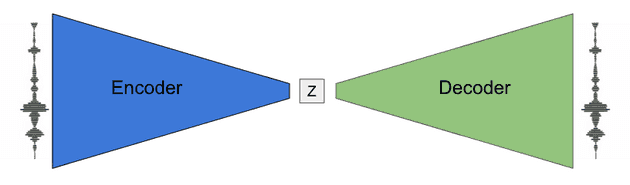
自动编码器(Auto Encoder: AE)通过学习将每个示例压缩(编码)为数字向量(隐代码或 z),然后从该数字向量复制(解码)相同的示例,从而构建数据集的隐空间。AE 的一个关键组成部分是通过使向量的维数小于数据本身而引入的瓶颈,这迫使模型学习压缩方案。在此过程中,自动编码器理想地提取整个数据集中常见的质量。NSynth 是自动编码器的一个示例,该编码器已学习音符音频中的隐音色空间:
这种类型的自动编码器的一个限制是它的隐空间中经常有“洞”。这意味着,如果你解码一个随机向量,它可能不会产生任何真实的结果。例如,NSynth 能够重建和插值,但由于这些“洞”,它缺乏真实感特性,因此无法随机采样。
另一种不受此问题影响的实施瓶颈的方法是使用所谓的变分损失 (Variation Loss)。不限制向量的维数,而是鼓励编码器产生具有预定义结构的隐代码,例如来自多元正态分布的样本的隐代码。然后,通过构造具有这种结构的新代码,我们可以确保解码器产生真实的内容。
SketchRNN 是变分自动编码器(VAE)的一个示例,它学习了以笔划序列表示的草图的隐空间。这些笔划由双向递归神经网络(RNN)编码,并由单独的 RNN 进行自回归解码。正如我们在上面看到的,这个隐空间拥有我们想要的所有属性,这部分要归功于变分损失。
循环乐段隐空间
对于 MusicVAE,我们从一个与 SketchRNN 非常相似的架构开始,学习循环乐段的隐空间,该空间包含所有期望的属性。我们在这里用几个例子来说明我们的结果。
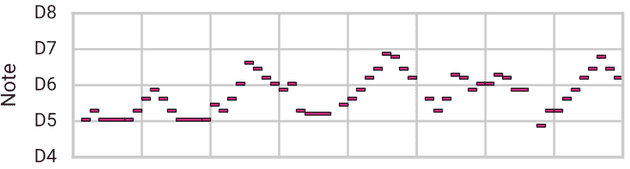
首先,我们将展示我们在两个序列之间变形的能力,虽然我们在文章的开头展示了一个混合两种旋律的例子,但让我们做一些更难的事情,将低音线变形为旋律 (from a bassline to a melody):
Bassline
Melody
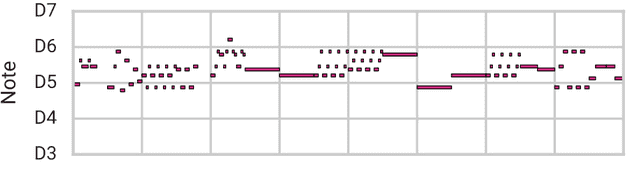
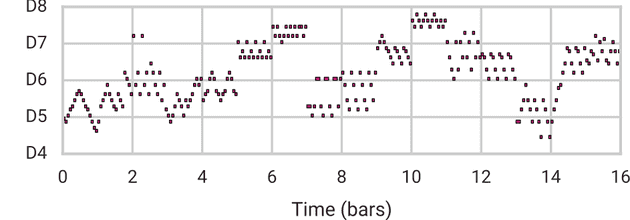
我们将首先尝试在不使用 MusicVAE 的情况下,通过简单地采样两者之间的音符,类似于音频中的交叉衰落,从低音线平滑地变形到旋律。下面你可以看到和听到这个初始的插值结果。第一段(黑色)是低音线,最后一段(黑色)是旋律。红色部分是插值的第一步,紫色部分是最后一步。每段 4 秒(2 小节)。
Data Space Interpolation (not MusicVAE)
Latent Space Interpolation (MusicVAE)
请注意,中间序列现在是有效的,它们之间的过渡是平滑的。中间序列也不像以前那样局限于从原始序列的音符中进行选择,然而音符选择在端点的上下文中更有音乐意义。在这个例子中,我们完全满足表达,真实感和平滑性的属性。
下面的视频是一个鼓点集合的例子:
长期结构 Long-Term Structure
语言模型(如 MelodyRNN 和 PerformanceRNN)的不足之处之一是它们生成的输出通常缺乏连贯的长期结构。正如我们之前用 SketchRNN 展示的,一个隐空间模型可以编码长期结构来产生完整的草图。
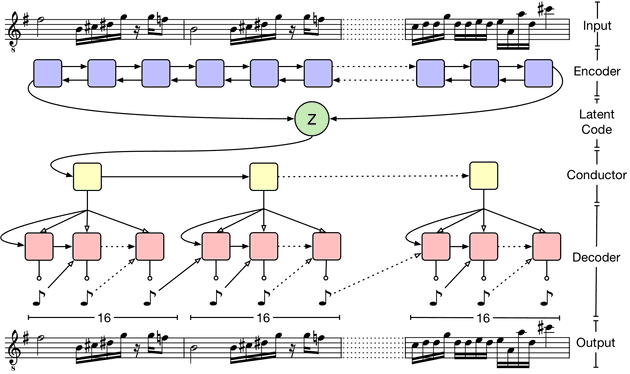
然而,为了在长音乐序列中获得类似的结果,我们发现我们不能依赖于相同的架构,长音乐序列通常比草图有更多的步骤。相反,我们开发了一种新的分层解码器,能够从单个隐代码中生成长期结构。
我们不是使用我们的隐代码来直接初始化音符 RNN 解码器,而是首先将代码传递给“指挥”RNN,他为输出的每个小节输出一个新的嵌入。然后,音符 RNN 独立地生成 16 个小节中的每一个,条件是嵌入,而不是隐代码本身。然后,我们从音符解码器中进行自回归采样。
我们发现这种有条件的独立性是我们架构的一个重要特征。由于该模型不能简单地依靠音符解码器中的自回归来优化训练期间的损失,因此它更依赖于隐代码来重构序列。
使用这种架构,我们能够像以前一样进行重建、采样和平滑插值,但现在需要更长时间(16 小节)的旋律。这里,我们混合了示例旋律 A(上)和 B(下):
Melody A
Mean
Melody B
此外,我们可以使用属性向量算法(回想一下上面的“猫脸向量”)来控制音乐的特定质量,同时保留其许多原始特征,包括整体结构。在这里,我们展示了通过在隐代码中添加/减去“音符密度矢量”来调整旋律中音符数量的能力。
Subtract Note Density Vector
Original
Add Note Density Vector
噪起来!
说服我们自己(希望是你!)我们可以用短期和长期结构对单个仪器进行建模,因此我们调整了我们的分层架构,以对不同仪器之间的相互作用进行建模。在这些模型中,我们将每个嵌入传递到多个解码器,每个乐器或轨道一个解码器,而不是将嵌入从指挥传递到单个音符解码器。
通过在隐空间中表现短的多乐器排列,我们可以像处理单个旋律一样处理所有的操作。例如,我们可以针对 8 种完全不同的仪器中的任何一种,在两种 1-measure 排列之间进行插值。下面是隐空间中随机点对之间的两次插值的合成 audo,仪器由模型选择。每个点代表 2 秒(1 条)。
我们还可以在 16 小节的基础上,将跨越小节的层级重新添加到模型 3 规范乐器(旋律、低音和鼓声)中。我们“三重奏”模型中的样本播放列表表明,它已经学会了如何在长时间框架内模拟三种乐器之间的相互作用: